Referencias

Del todo al objeto a
Sesión del 13 de marzo de 1968

La ubicación de las citas es indicada con paginación de la edición Seuil

• "un psicoanálisis, tipo o no, es la cura que se espera de un psicoanalista" (212)
  Jacques Lacan, "Variantes de la cura tipo", Escritos 1, Editorial Siglo XXI, página .

• "lo que quiso llamarse la unidad de la psicología" (213)
  Daniel Lagache, "L'unité de la psichologie", "La unidad de la psicología" (capítulo 2 "Psicología experimental y psicología clínica" y conclusiones).

• "el hombre piensa con su alma" (214)
  En De Anima I, 4, 408b11-15, Aristóteles dice: "No es el alma la que teje o la que construye casas, sino el hombre con (τῇ ψυχῇ) el alma", "οὐδὲ τὴν ψυχὴν ὑφαίνειν ἢ οἰκοδομεῖν, ἀλλὰ τὸν ἄνθρωπον τῇ ψυχῇ".

• "gnôthi seautón" (216)
  Gnôthi seautón (γνῶθι σεαυτόν) es una frase en griego clásico que significa "Conócete a ti mismo". 
  Es una máxima filosófica que estuvo inscrita en el pronaos del templo de Apolo, en el antiguo santuario griego de Delfos.

• "Begriffsschrift" (218)
  "Begriffsschrift", cuya traducción sería "Conceptografía" ("Begriffs schrift" - "escritura conceptual") , es un libro bastante pequeño (de solo unas ochenta páginas), del matemático y filósofo Gottlob Frege, sobre lógica. Fue publicado en 1879 con el subtítulo "Eine der arithmetischen nachgebildete Formelsprache des reinen Denkens" ("Un lenguaje de fórmulas, semejante al de la aritmética, para el pensamiento puro") y es ampliamente considerado como la publicación más importante en el campo de la lógica desde el Organon de Aristóteles. En este libro, Frege logró por primera vez formalizar la lógica clásica de predicados y, por lo tanto, la primera formalización de una lógica en la que una parte suficientemente grande de las matemáticas, pero también del lenguaje natural, podría expresarse. Junto con el Análisis matemático de la lógica de George Boole de 1847, el término "escritura" marca el comienzo de la lógica formal moderna. El término "escritura" también se usa para el cálculo lógico definido por Frege y para la notación lógica de Frege. Frege diseñó el término "escritura" para apoyar su investigación sobre los fundamentos de las matemáticas. El cálculo de Frege introdujo el cuantificador universal y los predicados de lugares múltiples por primera vez.
  Gottlob Frege, "Los fundamentos de la aritmética", "Ensayos de semántica y filosofía de la lógica", "Escritos sobre lógica, semántica y filosofía de las matemáticas", "Correspondencia Gottlob Frege - Bertrand Russel".

• "lo que llamamos la implicación filoniana" (219)
  La implicación "filoniana" es la interpretación lógica del condicional "si p entonces q", también conocida como "implicación material". 
  Esta forma de entender el condicional, atribuida a Filón de Megara, significa que un enunciado condicional es verdadero en todos los casos, excepto cuando el antecedente (p) es verdadero y el consecuente (q) es falso

• "distinguir dos formas de implicación diferente" (220)
  La distinción de las dos formas de implicación resultan de si el condicional se ubica "al nivel donde la proposición de plantea como asetórica", o "al nivel de la proposición ella misma".
  El esquema para la primera opción es:
  
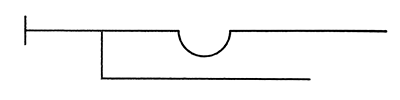
  Y el esquema para segunda opción debería ser:
  
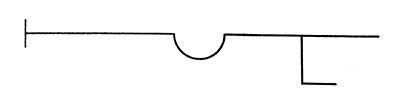
  Sin embargo Seuil reproduce el siguiente esquema, evidentemente erróneo, puesto que está ubicando dos incidencias condicionales
  
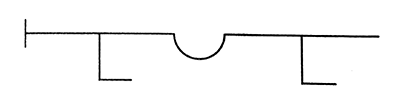
  La eventual "razón" de este "error" podría ser que el mismo ya se encuentra en la estenotipia.
  O quizás por el eventual malentendido que podría generar el párrafo siguiente cuando transcribe que no es lo mismo decir "si una cosa...." que "si otra cosa..". Sin embargo queda claro el error en el párrafo siguiente cuando señala que la distinción de la ubicación de los condicionales permite apreciar la función del hueco de "aislar y dar cuerpo al todo".

• "¬ꓱx.Fx, o existe x que haga la función Fx falsa, fórmula donde figura un doble menos " (222)
  Parece que debería escribirse ¬ꓱx-Fx para dar cuenta del "doble menos".
  Esta aparente incongruencia se explicita en la sesión anterior (página 206 de Seuil), señalando que la doble negación se expresa en la formulación lingüística.
  La aplicación de la negación en cada uno de los cuantificadores es diferente, ya que no es lo mismo la negación del cuantificador de la existencia ꓱx que la del "para todo" Ɐx.

• "la función opuesto del pan o del pantes en griego se opone a la función de holos, como en latin, el omnis se opone al totum" (222)
  En Seuil transcriben "holon" en lugar de "holos" ("ὅλος") y "omme" en lugar de "omnis".
  ὅλος (hólos) es una palabra del griego antiguo que significa "todo", "entero" o "completo". Se utiliza para indicar una idea de totalidad e interconexión, donde todas las partes de un conjunto están relacionadas y son necesarias para formar la unidad completa.
  πᾶν (pân) significa "todo" o "universal". Se utiliza comúnmente como prefijo en palabras como "panteísmo" y "pandemia" para indicar totalidad, y en el nombre del dios griego "Pan", relacionado con la naturaleza y los pastores.
  Πᾶντές (pronunciado "pantes") es una forma del griego antiguo que significa "todos", "todos y cada uno", o "la mayoría", funcionando como un pronombre o adjetivo que se refiere a un grupo de personas o cosas

• "la universal afirmativa la plantea καθ όλον" (222)
  El griego es "κατα χολου είπον αρετήé περι χω τηεστιν" ("kata holou eipôn aretès peri ho ti estin"), palabra por palabra: "teniendo en cuenta la totalidad para decir sobre aretès lo que es".
  La formulación utilizada aquí introduce otra expresión, que se popularizaría con Aristóteles,"κατά κώλου" ("kata holou"). Este es el único uso de esta expresión en todos los diálogos. Las formas ligeramente diferentes, con "κατά" y el acusativo "óλου" en lugar del genitivo όλον usado aquí, se encuentran en República, III, 392d9 (donde Sócrates dice que, para hacer mejor entendida su crítica de los poetas, no tratará el problema "kata holo"n, "según el todo", es decir, "en general", sino "tomando una parte", es decir, en ejemplos); en Parménides, 138e6-7 (kata holon) y 144e9 (kata a holon), en las discusiones de Parménides sobre el "uno" en relación con los conceptos de todo y partes; y en Timeo, 40a7 (donde habla de la creación del universo de tal manera que es «kosmon... kath' holon», es decir, «ordenado en su totalidad») y 55e7 (para hablar de uno de los triángulos elementales que es «más estable kata merè kai kath' holon», es decir, «según la parte y según el todo»). Pero en ninguno de estos otros usos la expresión tiene la connotación casi «técnica» que tiene aquí, anticipando el significado que adoptará en Aristóteles, en la forma agregada en una sola palabra, katholou («καθόλου»), que se convertirá para él en el término predilecto para designar lo «universal» en oposición a lo particular (nota tomada de Bernard Suzanne, Menón, 77a5-80d1)

• "Otto Rank" (224)
  Otto Rank, "Le traumatisme de la naissance", "El trauma del nacimiento"

• "el mito de Er" (226)
  El mito de Er es una alegoría filosófica de Platón, narrada por el guerrero Er, que relata su viaje al más allá tras una muerte clínica, su posterior resurrección y el mensaje que trae a la humanidad sobre el ciclo de la vida, muerte y reencarnación. Describe un juicio de las almas, la recompensa o el castigo según la virtud o el vicio en la vida terrenal, la elección de la próxima existencia en una llanura cósmica, y el olvido final antes de renacer en la Tierra, enfatizando la importancia de la justicia para el alma
  El "mito de Er" ocupa los últimos párrafos de "La República",
  Platón, "Mitos".