Notas y comentarios
Sesión del 6 de marzo de 1963

Esquema de la división subjetiva

Al comentar la sesión del 23 de enero, hicimos un repaso de las variaciones que el esquema de la división subjetiva va teniendo desde su primer versión en la sesión del 21 de noviembre de 1962 y la que se presenta en esta sesión del 6 de marzo de 1963 (ver notas y comentarios), donde se explicitán las consecuencias de la "invención" del objeto a en la sesión del 9 de enero de 1963. Concretamente: la inversión de la posición del objeto en relación al deseo, la posición primera del objeto a respecto de la división subjetiva $ en el esquema, tal como se presenta en la página 175 de la edición Paidos

Esquema sesión del 21 de noviembre 1962 Campo del Otro   Campo del Sujeto Primer esquema de la división subjetiva (sesión del 21 de noviembre de 1962) (página 36 de Paidos)

Esquema sesión del 6 de marzo 1963 Campo del Otro ------- Campo del Sujeto Tercer esquema de la división subjetiva (página 175 de Paidos)

En esta sesión, lo mismo que en la del 21 de noviembre, Lacan hablará del objeto a como "resto" de una operación. Pero las cosas ya no son exactamente igual.

En la sesión del 21 de noviembre, la división de A por S daba como cociente, con un primer "resto" $, cuya segunda división por S, dejaba el "resto" definitivo a.
El sujeto se inscribe como un "cociente" respecto al Otro ( el , "lo que me constituye como inconsciente"), "está marcado por el rasgo unario del significante en el campo del Otro", y el a es el "residuo de la puesta en condición" (1) del sujeto (es decir, de la segunda división de $ por S)
En cambio, ahora, la división de A por S sigue dando como cociente, pero con un primer resto a, cuya segunda división por S nos da como "resto" definitivo $.
Este "resto" pasa a ser "lo irreductible del sujeto" (2) y asume una posición anterior: "el a es lo que permanece irreductible en la operación total de advenimiento del sujeto al lugar del Otro, y ahí es donde adquirirá su función" (3).
La relación de a con S (el sujeto del nivel mítico anterior a la operación del significante) - donde a es "aquello que representa al S en su real irreductible" (4) - es lo que completa la operación de la división (ya que el A no tiene común denominador con respecto a a y S), obteniendo como resto final el $.

Obviamente, no se trata de una división aritmética en sentido exacto (5) sino de una analogía destinada a ordenar la operación interrogativa en A y ubicar la diferencia que surge entre el "A-respuesta" (el A marcado por la interrogación, ) y el "A-dado" (el A inicial, el tesoro del significante), "algo que es el resto, lo irreductible del sujeto" (6), el a.

A continuación, Lacan completa este cuadro, con una tercera columna, donde caracteriza cada uno de los pisos del esquema.

Tercer esquema (ampliado) de la división subjetiva
(página 176 de Paidós)

Asi tendremos, "al principio una x que solo podemos nombrar retroactivamente, que es, propiamente hablando, el acceso al Otro, el punto de mira esencial en que el sujeto debe situarse", al que sigue "el nivel de la angustia, constitutivo de la aparición de la función a", y finalmente, "el $ como sujeto del deseo" (7)

Asumiendo "la abstracción, sin duda extrema", que acaba de articular, Lacan se propone devolvernos a "la evidencia de la imagen", con la legitimidad que implica el hecho mismo de que "eso irreductible del a es del orden de la imagen" (8), lo cual nos lleva a la función de la caída del objeto (ver notas y comentarios)

Notas

(1) Jacques Lacan, El Seminario, Libro X, La angustia, Editorial Paidos, página 36.

(2) Idem, página 175

(3) Idem

(4) Idem

(5) Recordemos los términos de la división aritmética

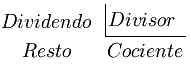
cuya operación consiste en averiguar cuántas veces un número (el divisor) está contenido en otro número (el dividendo). Al resultado entero de la división se denomina cociente y si la división no es exacta, es decir, si el divisor no está contenido un número exacto de veces en el dividendo, la operación tendrá un resto o residuo.

En ese sentido, si por un lado puede ser válido decir que "este a sobre S es lo que completa la operación de división", es incongruente, matemáticamente hablando, decir que "$ es equivalente a a sobre S" (subrayado mío), primero porque $ es el resto y no el cociente de la división: "a sobre S" (el cociente de este segundo paso serían los decimales que habría que agregar al cociente del paso anterior ()), y segundo, porque la división "a sobre S" solo podría tener una "equivalencia" (igual valor) si su resto fuera cero.

En otras palabras, esta es otra de las páginas a las que los Sokal (ver debate) o Martinez podrían apelar para "denunciar" el uso "incorrecto" de las matemáticas por parte de Lacan.

(6) Jacques Lacan, op. cit., página 175

(7) Idem, página 176

(8) Idem