 |
 |
 |
 |
Referencias
De la incomprensión y otros temas
Charla en Sainte Anne del 2 de diciembre de 1971
La ubicación de las citas es indicada con número de página de la edición Paidós "Hablo a las paredes"
"Cuando fui a la Sociedad de Fisolofía para presentar una comunicación" (52)
Jacques Lacan, "Subversión del sujeto y dialéctica del deseo en el inconsciente freudiano", Escritos 2, Editorial Siglo XXI.
"en algún lado del último número de mi revista Scilicet" (53)
El 1970 fue publicado el combinado de los números 2 y 3 de la revista Scilicet, dirigida por Lacan (el primer número fue publicado en 1968, y el cuarto, recién en 1973),
En ese número doble (2-3) se incluye el texto "Radiofonía":
"Psicoanalista, es del signo que estoy advertido. Si me señala alguna cosa de la que me debo ocupar, por haber encontrado la lógica del significante para romper el señuelo del signo, yo sé que esa alguna cosa es la división del sujeto: la cual división aspira a que el otro sea lo que constituye el significante, por lo que no podría representar a un sujeto sino a no ser uno más que del otro".
"el hecho de que haga falta que sea a sabiendas como él interprete" (negritas mías) (55)
En francés es "le fait qu'il faille bien que ce soit à son su qu'il interprète" (página 40 de la edición de Seuil).
No creo que "a sabiendas" sea la mejor traducción para "à son su". La traducción literal es "su sabido". Puede resultar un poco rara semánticamente, pero es más precisa en relación a "su" saber que, veremos, es supuesto.
"Bertrand Russel (..) la matemática se ocupa de enunciados de los que resulta imposible decir si tienen una verdad, ni siquiera si tienen algún significado" (61)
Bertrand Russell, "Mysticism and Logic", "Misticismo y lógica"
"Pure mathematics consists entirely of assertions to the effect that, if such and such a proposition is true of anything, then such and such another proposition is true of that thing. It is essential not to discuss whether the first proposition is really true, and not to mention what the anything is, of which it is supposed to be true. [...] Thus mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true. People who have been puzzled by the beginnings of mathematics will, I hope, find comfort in this definition, and will probably agree that it is accurate",
"Las matemáticas puras consisten enteramente en afirmaciones en el sentido de que, si tal o cual proposición es verdadera de algo, entonces tal o cual otra proposición es verdadera de esa cosa. Es esencial no discutir si la primera proposición es realmente verdadera, y no mencionar qué es la cosa de la que se supone que es verdadera. [...] Así, las matemáticas pueden definirse como la materia en la que nunca sabemos de qué estamos hablando, ni si lo que estamos diciendo es verdad. Las personas que han estado desconcertadas por los comienzos de las matemáticas, espero, encontrarán consuelo en esta definición, y probablemente estarán de acuerdo en que es precisa."
"matemas" (64)
"Mathème" es un neologismo que Lacan inventa en este momento, en forma de sustantivo, a partir de "mathématique", que a su vez deriva del griego antiguo "μάθημα", "mathêma", que significa "ciencia". Se ha traducido al castellano como "matema".
Servirá para designar la formalización algebraica de los conceptos del psicoanálisis con miras a su transmisión.
En esta misma conferencia indicará que no se justifica "hablar del matema como algo que estaría separado de la exigencia de verdad" (página 65), y que "el matema, aunque lo abordemos por las vías de lo simbólico, no deja de ser real" (página 67). .
Roudinesco, en su "Diccionario de psicoanálisis" (junto con Michel Plon) ha fabulado su propia versión de origen, según la cual estaría "construido a partir del mitema de Claude Lévi-Strauss y del griego antiguo μάθημα, conocimiento, no pertenece específicamente al campo de las matemáticas" (fabula que, obviamente, es la historia más difundida).
“la matemática griega (...) tuvo posibilidad de acercarse a lo que se produjo en el momento del surgimiento del cálculo infinitesimal” (64)
El método de exhaución es un procedimiento geométrico inventado por los griegos mediante el cual podemos aproximarnos al perímetro o al área de figuras curvas, aumentado la precisión de la aproximación conforme avanzamos en el cálculo. Eudoxo (408−355 a. C.) usó este método para encontrar el área de una forma inscribiendo dentro de ella una secuencia de polígonos cuyas áreas convergen al área de la forma que la contiene. Pero el desarrollo más conocido de este método es el de Arquímedes (287−212 a. C.) para aproximar el área de los círculos con polígonos regulares inscritos y circunscritos, y como esa propiedad se cumplía para los polígonos entonces se deducía que se cumplía para los círculos.

Este original método "mecánico", que permitía hallar el área del círculo, la longitud de la circunferencia y, como consecuencia, el número pi, permitía también saltar la prohibición aristotélica de usar el infinito in acto.
En efecto, ante la imposibilidad de negar los procesos infinitos, Aristóteles trató de regularlos; para ello prohibió el infinito en acto: "no es pasible que el infinito exista como un ser en acto o como una sustancia y un principio", leemos en el libro III de la Física. Pero, como él mismo reconoce poco después, "es claro que la negación absoluta del infinito es una hipótesis que conduce a consecuencias imposibles", de manera que "el infinito existe potencialmente", esto es, "el infinito es o por adición o por división", o de otra forma, "la magnitud no es actualmente infinita, aunque infinitamente divisible". Así, por ejemplo, la regulación aristotélica impide considerar un segmento como una colección de infinitos puntos alineados, pero sí permite divisiones del segmento por la mitad, digamos, tantas veces como se quiera. El infinito potencial de Aristóteles es, pues, definido como atributo: la posibilidad de ir más allá de cualquier límite -considerando, por ejemplo, números más grandes que uno dado.
En cambio, el infinito en acto debería ser entendido como una negación, es lo que no tiene límites.
Estas regulaciones conforman razón principal de ese no franqueamiento del paso que señala Lacan.
“Isaac Barrow” (65)
Isaac Barrow fue un teólogo, profesor y matemático británico. Barrow es famoso por haber sido el primero en calcular las tangentes de la curva kappa (un tipo de curva algebraica de dos dimensiones, cuya forma se asemeja a la letra griega ϰ "kappa").
Isaac Newton fue discípulo de Barrow.
“la efracción cantoriana (...) la dimensión patética que en Cantor llegó hasta la amenaza de locura” (65)
Georg Ferdinand Ludwig Philipp Cantor fue inventor con Dedekind de la teoría de conjuntos, que es la base de las matemáticas modernas. Gracias a sus atrevidas investigaciones sobre los conjuntos infinitos fue el primero capaz de formalizar la noción de infinito bajo la forma de los números transfinitos (cardinales y ordinales).
Vivió aquejado por episodios de "depresión", atribuidos originalmente a las críticas recibidas y sus fallidos intentos de demostración de la hipótesis del continuo, aunque actualmente se cree que sufría algún tipo de "enfermedad maníaco-depresiva". Murió de un ataque cardíaco en la clínica psiquiátrica de Halle. En el número 10 de "Cahiers pour l'analyse" se publico la traducción al francés de "Fondements d’une théorie générale des ensembles" (hay traducción al castellano "Fundamentos para una teoría general de conjuntos").
Recomiendo el libro de Natalie Charraud "Infini et inconscient : essai sur Georg Cantor". "
“diálogos socráticos (...) el encuentro con el pez torpedo” (66)
En el Menón, este le dice a Sócrates: "Había oído decir, Sócrates, antes de conversar contigo, que tú no sabias más que dudar y sumir a los demás en la duda; y veo ahora que fascinas mi espíritu con tus hechizos, tus maleficios y tus encantamientos; de manera que estoy lleno de dudas. Y si es permitido chancearse , me parece que imitas perfectamente por la figura y en todo, a ese corpulento torpedo marino, que causa adormecimiento a todos los que se le aproximan y le tocan".
“Picasso decía yo no busco, encuentro” (71)
La fuente más frecuente para esta conocida frase atribuida a Picasso es el libro de Carlos Pérez-Bermúdez, "Lo que enseña el arte: La percepción estética en Arnheim", Ed. Universitat de València.
“les habría mostrado la pequeña vueltita que en alguna parte lo convierte en el discurso del capitalista” (73)
Lacan todavía no dio la conferencia en Milan donde escribe el esquema con los cambios de letras con los que define el discurso del capitalista (esa conferencia será al año siguiente, el 12 de mayo de 1972)
¿Ya lo tiene en vista, cuando habla de "la pequeña vueltita"?
“lo dicho, dicho está, escribí en la primera frase de algo que estoy excogitando para entregárselo más adelante” (74)
Clara referencia al texto "L'Etourdit" , publicado en el número 4 de la revista Scilicet (1973) e incluido luego en "Autres Ecrits", "El atolondradicho", publicado en el primer número de la revista Escansión, e incluido en "Otros Escritos", Editorial Paidós, páginas 473-522) donde, no en la primera frase, pero si al comienzo, luego de ciertas presentaciones, escribe: "que se diga queda olvidado tras lo que se dice en lo que se oye"
“l'hachose” (74)
Otro neologismo creado en esta ocasión, en el que retoma el neologismo "achose" (introducido en la sesión del 8 de abril de 1970 - Radiofonía - del seminario XVII "El envés del psicoanálisis", para transformar "la chose", "la cosa", en "l'achose", "la a-cosa"), agregándole una "h" para marcar el apóstrofe tras la "l".
“hacer un tetraedro con esos cuatro discursos” (77)
Lacan retomará esta relación de los discursos con el tetraedro en la charla del 3 de febrero de 1972 en Sainte Anne, incluida en la edición del seminario XIX con el título de "Topología de la palabra".
El tetraedro es uno de los cinco poliedros regulares (sus caras son polígonos regulares y constituyen una superficie orientable, es decir, bilátera), también llamados "platónicos" (tetraedro, cubo, octaedro, dodecaedro e icosaedro) eh homenaje a Platón quien, en sus diálogos con Timeo (convocado por sus conocimientos en asotronomía y naturaleza del universo) extrae la génesis del mundo a partir de esas cinco figuras perfectas. En el tetraedro, en tanto superficie orientable (dos caras),a cada vértice llegan tres vectores y de ahí mismo parten 3 vectores.
La construcción que hará Lacan pasa por restringir los vectores orientados a solo 3 por vértice. El resultado de esta operación, traslada al plano, nos da un cuadrípedo, sobre el que desplegará los términos de la estructura de los discursos (y excluirá un vector más, el que conectaría la verdad desde el plus de gozar) 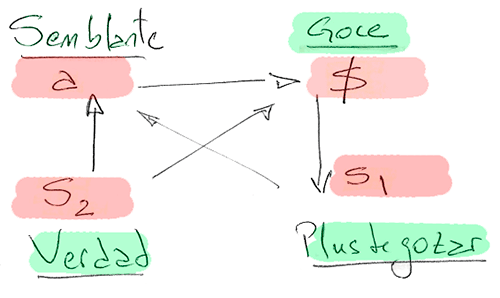
“la ciencia y la verdad” (82)
Jacques Lacan, "La ciencia y la verdad", Escritos 2, Editorial Siglo XXI.